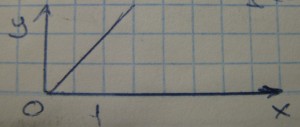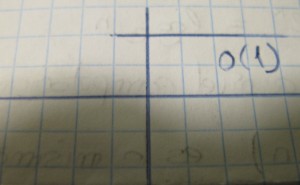Jun 16
Algoritmia
Esta seccion abarca todo lo relacionado con algoritmos y estructuras dinamicas de datos, asi como las notaciones empleadas a modo lenguaje para poder analizar las distintas opciones.
LAMBDAU
- Una funcion f es O(g) si |f| <= M|g|
- Si f es mas lento cuando tiende a infinito que una constante de otra funcion es bueno.
- Orden n es O(n), cualquier funcion que crezca mas lento que una recta.
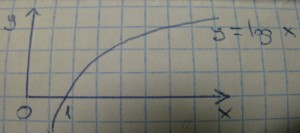
– O(lg n) como por ejemplo la busqueda binaria.
n / 2 n / 4 n / 8 n / 2 elevado k
(Nos queremos queda en 1 elemento n / (2 elevado k) = 1)
Para despejar k hayy que hacer logaritmo en ambos lados.
log2 2^k = log2 n ; k = log2 n
Aunque a nivel computacional cuesta lo mismo log2 log10 logn
O(log n) es lo mismo que O(n^2)
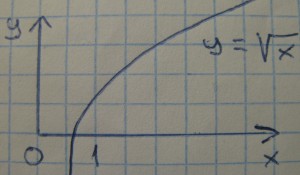
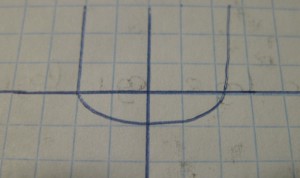
– O(√n) como por ejemplo ver si un numero es primo.
Si es div 2 si es div 2
Si es div 3 » si es div 3
Si es div 4 si es div 4
... ...
En vez de parar de buscar en n-1 paramos en √n
(ya que ningun numero que hay por encima sera divisor)
Crece un poco mas rapido que la logaritmica
– O(n) como por ejemplo la busqueda de un valor con un for en un array desordenado.
– O(n log n) como por ejemplo el algoritmo quicksort (indicar que es mejor que n²)
– O(n³)
– O(2 elevado n)
– O(n!) como por ejemplo la factorizacion de enteros.
Otros tipos de crecimiento son:
- Cuadrado
- Cuadratica constante O(1)
Para ello la base ha de ser:
– positiva b > 0
– distinta a 1 b ≠ 1
Definicion: A que numero debo elevar la base para que me de N.
log b N
log b N = x ] vista logaritmica
b elevado x = N ] Vista exponencial
<en desarrollo>