ελευθερία ϗ ἀλήθεια

Listado de libros técnicos:

A continuación ire publicando la lista de libros que considero que son bastante iluminadores a nivel de conocimiento en el ámbito técnico:

Operating system:

• Linux Edicion especial
• Linux Kernel Development
• The Linux programming interface
• Unix Network Programming Vol I: The sockets networking API
• Unix Network Programming Vol II: IPC
• TCP/IP Illustrated Vol 1
• TCP/IP Illustrated Vol 2
• TCP/IP Illustrated Vol 3
• Programming with POSIX Threads
• Advanced Programming in the UNIX Environment

Networking:

• Computer Networks
• DNS and BIND
• Understanding Linux Network Internals
• Ethernet
• Wifi 802.11

Programacion:

• Analysis Patterns
• Design Patterns
• Extreme programming explained
• Refactoring
• Applying UML and patterns
• The Pragmatic Programmer
• Introduction to Algorithms
• The art of computer programming Vol 1
• The art of computer programming Vol 2
• The art of computer programming Vol 3
• ASM
  • x64 Assembly language step-by-step
  • Beginning x64 Assembly programming
  • Modern x86 assembly language programming
• C
  • The C Programming Language
  • Mastering Algorithms with C
• C++
  • The C++ programming language
  • Modern C++ design
  • C++ Coding standards
• Lisp
  • Structure and Interpretation of Computer Programs
  • Land of Lisp
  • The little schemer
  • Common Lisp

Security:

• Wireshark network analysis
• Nmap network scanning
• Metasploit
• Stealing the network
• Hacking
• Applied Cryptography
• Rootkits
• Exploiting software
• Firewalls Linux
• Reversing
• Shellcoder’s handbook
• Linux Maxima Seguridad

Tooling:

• Pro Git
• An introduction to GCC
• Managing projects with GNU Make
• Autotools
• The art of debugging: GDB and DDB
• Sed and AWK
• Valgrind
• Learning GNU Emacs

Logical:

• Gödel, Escher, Bach: un Eterno y Grácil Bucle de Douglas Hofstadter

1. Gödel, Escher, Bach: un Eterno y Grácil Bucle de Douglas Hofstadter

Orientada al analisis de sistemas formales, derivacion de teoremas, axiomas, teorema de incomplentitud de Godel, etc. Se centra en la lectura y analisis del libro GEB; Godel, Escher, Bach: un eterno y gracil bucle. Los temas tratados en el libro no tienen una relacion directa con emacs o el lenguaje lisp, pero si una indirecta, de hecho en el libro se trata y analiza el lenguaje lisp. Por lo que es interesante el analisis de la totalidad del libro y no queria crear un nuevo blog solo para esto, aprovechando asi este por su estrecha relacion. Ire anadiendo aqui mis apuntes a medida que progrese con la lectura. Mi analisis, asi como algunos apuntes pueden ser algo esquematicos, con cambios repentinos de ideas, etc. Asi que advierto al lector que no tome ellos como una lectura sino como referencia una vez haya leido previamente dichos capitulos.

Antes de comenzar debemos tener claras unas ideas basicas, tanto para leer este libro como para analizar problemas de la vida real, y esto es una afirmacion propia:

«El analisis y la capacidad de abstraccion de los matematicos estan un nivel por encima del resto de la humanidad, a partir de ahora tendreis que cambiar la forma de razonar. Las matematicas no son una ciencia, porque las ciencias son empiricas, o lo que es lo mismo, en el conocimiento basado en la experiencia (y por lo tanto jamas demostrables). En cambio las matematicas son deductivas, ya que son secuencias finitas de formulas  que son axiomas o inferencias directas a partir de formulas previas.«

Sin mas dilacion, comienzo mi analisis:

Analisis de la introduccion (Ofrenda musico-logica):

El piano forte remedia el problema de otros instrumentos que no permitian que las teclas pudiesen sonar mas o menos fuerte que sus vecinas.

Regis Iusfu Cantic Et Reliqua Canonica Arte Refotula -> RICERCAR (que significa indagar). Dicha frase en latin significa «Por orden del Rey, la cancion y el resto resueltos con arte canonico«. El canon sirve de melodia y acompanamiento.

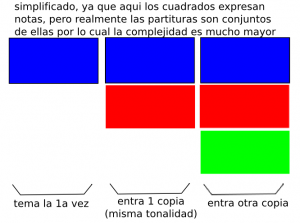
Los 10 canones de la Ofrenda Musical mas elaborados, pero con presentaciones incompletas, los temas escritos y acompanados de indicaciones enigmaticas para descubrir el canon basado en ese tema.

• El canon circular:

3 voces canonicas, donde cada nota del tema necesita funcionar de 2 maneras armonicas distintas y conservar su funcion melodica al mismo tiempo (sentido musical).

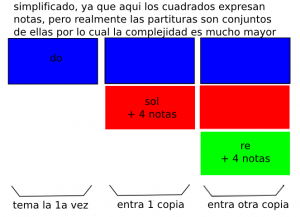
• 1er grado de escala de complejidad:

Escalonan no solo en tiempo sino tambien en tono.

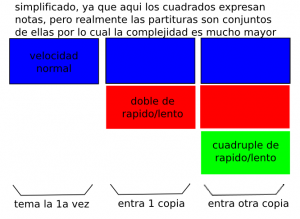
• 2o grado de escala de complejidad:

Si es mas rapido se denomina aumentacion y si es mas lento se denomina disminuicion.

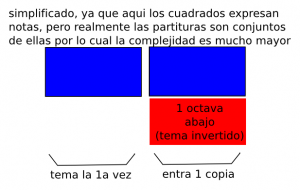
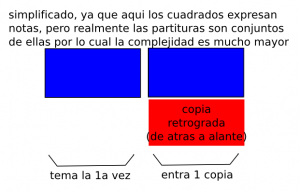
• 3er grado de la escala de complejidad (tema invertido):

Tema invertido debido a que cada copia entra con 1 octaba por debajo del tema original.

• 4o grado de la escala de complejidad (esoterica – canon cangrejo):

Canon cangrejo por la curiosa capacidad motriz de estos crustaceos.

Las copias mantienen toda la informacion del tema original (el tema original es recuperable a partir de sus copias (isomorfismo) lo cual aumenta la belleza de la obra.

Aclaro distintos conceptos antes de continuar; cuando distintas voces que van entrando por ejemplo cambiando 4 tonos por encima o con cualquier complejidad de las citadas arriba y este es menos rigido (cuando entran todas no hay ‘formulas’) se denomina fuga, mientras que si es mas rigido se denominara canon.

Y aqui podemos ver el resultado de manera representada de forma visual, para que nos hagamos una idea de la complejidad del asunto:

J.S. Bach – Crab Canon on a Möbius Strip

Cita de Godel: una proposicion de la teoria de numeros no habla de una proposicion de la teoria de numeros, es solo una proposicion de teorias de numeros.

Concepto de demostracion: son pruebas dentro de sistemas fijos de proposiciones.

Aseveracion Epimenides -> Paradoja (no es ni verdadera ni falsa).

Aseveracion G de Godel -> Indemostrable (dentro de la Principia Mathematica) pero verdadera.

Conclusion: Principia Mathematica -> Incompleto.

Analisis del Capitulo I: El acertijo MU (sistemas formales)

Convenciones:

• Entre comillado doble («) se refieren al mismo texto a todo.
• Extre comillado simple (‘) se refiere a la cadena entrecomillada.

Un sistema formal no se debe proceder al margen de las reglas, esto es un requisito de formalidad.

• Regla I: Cadena acabada en letra «I» se puede agregar una «U» al final.
• Regla II: Cadena ‘Mx’ se puede agregar ‘Mxx’ a la coleccion.
• Regla III: Si en una cadena aparece la secuencia «III», esta puede substituirse por «U».
• Regla IV: Si aparece «UU», esta permitida su eliminacion.

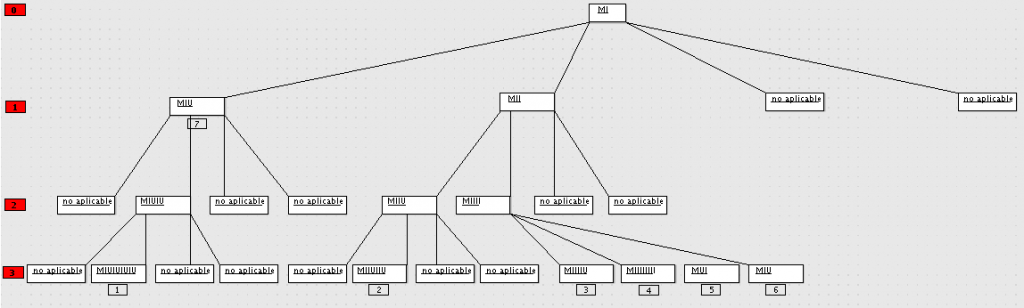
Derivo de forma grafica teoremas del sistema formal MIU a partir del axioma MI. Por la embergadura que conlleva he decidido realizarlo aplicando de forma mecanica (como si fuera un ordenador) todas y cada una de las reglas sin excepcion, aunque hare uso de mi razonamiento cuando encuentre ciertas caracteristicas al derivar (como un humano).

Notas y conclusiones:

0 Representa el axioma y 1, 2 y 3 representan niveles de derivacion habiendo aplicado las 4 reglas a cada teorema.

1. No tiene sentido seguir derivando a partir de esta teorema, ya que nos encontramos en un bucle infinito sin poder aplicar otras reglas.

6. Mismo teorema que el caso 7. (derivacion del axioma aplicando la primera regla del sistema formal). Redundante, por lo que no seguimos.

2. 3. 4. y 5. Seguimos derivando estos teoremas.

Notas y conclusiones:

3 (nivel ampliado del anterior grafico) y 4 representan niveles de derivacion habiendo aplicado las 4 reglas a cada teorema.

2. 3. 4. y 5 son los teoremas (mismos que en el anterior grafico del nivel 3, es decir que representa el mismo nivel).

8. Derivando este teorema se llega a un lugar sin salida, ya que solo sera posible aplicar esta regla de forma infinita, por lo que lo descartamos. Hemos descubierto un bucle infinito! estan por todos lados aunque no los veamos!

9. Carece de sentido aplicar la II regla y seguir derivando por este camino, ya que siempre habra 1 «I» en medio (antes de la «U»)ya que son 4 (pensar de forma matematica y sobre factorizacion y numeros primos y entendereis el por que). Lo mismo ocurre aplicando la III regla para derivar este teorema. Las reglas I y II no son aplicables. Por lo que descartamos este teorema.

15. Este teorema generado es el mismo que el 10. Ambos obtenidos de manera distinta, aplicando distintas reglas durante la derivacion. Asi que solo seguimos derivando con el 10. para evitar redundancia.

10. y 11. Existen dos teoremas derivados aplicando la tercera regla del sistema formal.

12. y 13. Nunca un 2 elevado a X sera multiple de 3 por tanto nunca podremos eliminar esas «I» para obtener «U» (pensar de forma matematica y de nuevo sobre la factorizacion y numeros primos y entendereis de nuevo el por que) y esto incluye a los teoremas aplicando las reglas I, II o III, para derivar. La cuarta regla no es aplicable. Por lo que descartamos este teorema y todos los derivados a partir de este.

14. Ademas permite aplicar la tercera regla del sistema formal de manera multiple, esto es que se pueden aplicar a distintas partes de la cadena, obteniendo mas de un teorema al aplicar esta regla derivando. Es exactamente el mismo caso que 10. y 11. sin embargo aqui obtenemos muchos mas teoremas.

10. 11. y 16. Seguimos derivando estos teoremas de momento.

Notas y conclusiones:

4 (nivel ampliado del anterior grafico) y 5 y 6 representan niveles de derivacion habiendo aplicado las 4 reglas a cada teorema.

10. 11. y 16. son los teoremas (mismo que el anterior grafico del nivel 4, es decir que representa el mismo nivel).

17. 18. 20. y 21. Continuamos derivando.

19. No tiene sentido continuar derivando este teorema devido a que es igual que el axioma (bucle infinito!) Descartamos pues.

22. No tiene sentido seguir derivando este teorema, ya que se combinaran 3 «U», «I», tampoco al principio se eliminaran las «I»intermedias (para alcanzar nuestro objetivo). Ademas nunca acabara en «I» por lo que nunca se substituira por una ‘U’ para que aparezcan 3 «U»s para poder eliminarlo y asi llegar al teorema que buscamos. Lo descartamos pues.

23. 26. 27. y 28. Es exactamente el mismo caso que 22. (el teorema en si es distinto, pero se aplican los mismos problemas que en el teorema ya citado). Lo descartamos entonces.

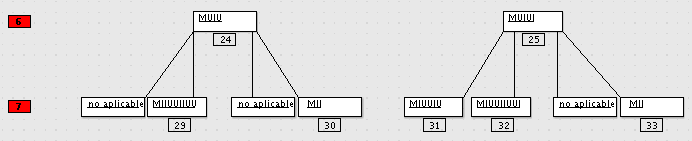
24. y 25. Se aplica en este caso la IV regla y se pueden obtener 2 teoremas distintos (dependiendo de donde se quiera aplicar el reemplazo). Continuamos derivando ambos teoremas.

Notas y conclusiones:

6 (nivel ampliado del anterior grafico) y 7 representa el nivel de derivacion habiendo aplicado las 4 reglas a cada teorema.

24. y 25. son los teoremas (mismo que el anterior grafico del nivel 6, es decir que representa el mismo nivel).

29. y 31. Llega a teoremas descubiertos en casos anteriores (algunos) pero otros no.

30. y 33. Mismo caso que aplicando la regla II al axioma original.

Llegando al septimo nivel de derivacion de todos los teoremas posibles, realizando este proceso de manera mecanica como si de un ordenador nos tratasemos, podriamos no terminar, sin embargo es dificil que no entremos a analizar este problema de manera razonada, pronto descubriremos distintos casos que son redundantes, que carece de sentido (expansion infinita) u otros empleando la imposibilidad de reduccion para conseguir el teorema final mediante la aplicacion de alguna regla, esta parte es la que diferencia como bien dice el libro entre maquinas y humanos. Es posible que existan maquinas o programas de ordenador que se programen para ‘percatarse’ de algunos de estos casos (como la redundancia), sin embargo no sera capaz de descubrir algunas otras (ya que requiere del razonamiento humano). Cuando realice por primera vez este acertijo, tuve el error de intentarlo de manera razonada, pero ante la embergadura de los teoremas derivables perdi el hilo y no fue la mejor manera de tratarlo, mas tarde lo realice de manera mecanica pero en un espacio demasiado pequeno como para poder proseguir y expandir mas de 2 o 3 niveles aplicando las 4 reglas posibles, finalmente decidi hacerlo en un monton de papeles, al menos para poder derivar hasta cierto punto donde mi cerebro pudo analizar de manera razonada ciertas coincidencias y asi resolver este problema.

Como colofon final podemos decir claramente que siempre volvemos a casos anteriores, que a su vez son recursivos (ya que volveremos de nuevo a esos mismos casos) y redundantes porque repetiremos las mismas reglas sin efecto distinto… mediante esta via razonada podemos probar que NO es posible decir MU.

Existen una serie de conceptos que antes no he aclarado y que podria ser interesante conocer antes de continuar:

• En los sistemas formales, las cadenas de simbolos generadas mediante el empleo de reglas se llaman teoremas.
• La acepcion de teoremas en matematicas son afirmaciones formuladas en lenguaje corriente cuya veracidad ha sido probada por medio de demostracion rigurosa (afirmaciones demostradas).
• Un teorema proporcionado de manera inicial en un sistema formal se denomina axioma.
• Todo sistema formal cuenta con; reglas de derivacion de simbolos que son denominadas reglas de produccion o reglas de inferencia.
• Una derivacion de un teorema es una demostracion explicita punto por punto del modo que es producido de acuerdo a las reglas del sistema forma.
• El concepto de probar y derivar son diferentes: no tiene sentido decir que probe «MUIIU» pero si que derive «MUIIU». En cambio si tiene sentido haber probado MU.
• El concepto de demostracion podria simplificarse con un ejemplo tal que todos los teoremas del sistema «MIU» deben comenzar con una «M».

Hemos usado reglas taquigraficas como ‘x’ para referirnos a un conjunto de cadena.

Existen modalidades de abordamiento en sistemas formales:

• Via M: Mecanica (se efectuan dentro del sistema).
• Via I: Inteligente (se efectuan fuera del sistema).

Tambien existe otro concepto importante y es el de estar dentro o fuera del sistema:

• Via U: Ultravia (via zen de aproximacion a las cosas).

Pasemos ahora a los procedimientos de decision con tendencias opuestas:

• Reglas ampliadoras (I y II del sistema formal MIU).
• Reglas reductoras (III y IV del sistema formal MIU).

Detectar los NO teoremas (como por ej. no comienza por M) es facil, pero quien dice que esto permitira detectar todos los no teoremas?

Si existe una prueba de teoremidad, una verificacion que se complete dentro de un finito este sera un procedimiento de decision del sistema formal tratado.

Si se necesita un lapso de tiempo infinito para una caracterizacion de todos los teoremas es que no es una caracterizacion lo bastante completa.

La diferencia entre conjunto de axiomas del conjunto de teoremas es que el conjuto de axiomas siempre esta dotado de un procedimiento de decision, que en el segundo puede faltar.

Analisis del Capitulo II: Significado y forma matematica

Problema filosofico: las palabras y los pensamientos estan regidos o no por reglas formales?

El sistema mg

El sistema formal ‘sistema mg‘ cuenta con 3 simbolos:

• m
• g
• –

Con infinitos axiomas, no se pueden contar todos, por lo que se necesita una descripcion de los axiomas, un metodo que nos indique si una cadena es o no un axioma. Queremos evitar un lapso prolongado o infinito para descubrir si cierta cadena es o no un axioma (como ocurria en el sistema MIU).

Definicion: xm-gx- es un axioma, siempre que x este compuesto solo por guiones.

Expresion: – -m-g- – – (axioma)

Expresion: xm-gx- (no es un axioma, ya que x no pertenece al sistema mg, sino que es una matriz que moldea todos los axiomas, a esto se le denomina esquema de axioma).

Regla: si x, y y z representan cadenas especificas por guiones:

• xmygz (teorema)
• xmy-gz (teorema)
• z vale –
• x vale – –
• y vale – – –

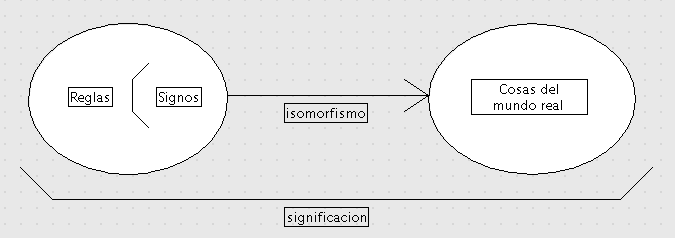
Isomorfismo

Isomorfismo (o nocion matematica): dos estructuras complejas son proyectadas una sobre otras, de tal modo que cada parte de una de ellas tiene su parte correspondiente en la otra. ‘Correspondiente’ aqui significa que ambas partes cumplen papeles similares en sus respectivas escrituras.

Hay un ‘nivel inferior‘ en nuestro isomorfismo, la proyeccion entre las partes de las dos estructuras.

• x <-> mas
• g <-> igual
• – <-> uno
• – – <-> dos
• – – – <-> tres
• <-> indica correspondencia (esta correspondencia es una interpretacion)

En un ‘nivel superior‘ se situa la correspondencia entre proposiciones verdaderas y teoremas. Puede no ser advertida (la correspondencia) sino se esteblece una interpretacion de los simbolos.

Interpretacion

Interpretacion no significativa: no se advierte la menor asociacion isomorfica entre los teoremas del sistema y la realidad.

Interpretacion significativa: los teoremas y las verdades se corresponden, es decir, existe isomorfismo entre teoremas y determinada porcion de la realidad.

Interpretacion vs significado: En el caso de interpretacion podria haber adoptado cualquier palabra de ‘m’ mientras que en el caso de significado, mas es la unica eleccion significativa.

El significado se puede referir en cuanto a sistema formal o en cuanto a lenguaje.

En el significado de lenguaje, el dominio del idioma que no se asemeja al de producto terminado. Mientras que en el significado de sistema formal, los teoremas son definidos a priori por las reglas de produccion y podemos elegir significados que se funden en isomorfismo (si lo encontramos) entre teoremas y proposiciones verdaderas.

En el sistema mg es posible (incluso deseable) que una cadena sea un teorema debido a los significados hablados por cada simbolo, cuando realmente no lo son. Seria un serio error que debe ser un teorema solo por su significado, no es siquiera correcto atribuirle un significado puesto que no es una cadena bien formada.

Un solo sistema formal puede ser isomorfico y asumir dos significados pasivos (esto lo veremos en el aspecto suma y resta del sistema mg). Una cadena bien formada en sistemas formales es aquella que al ser interpretada simbolo por simbolo porduce oraciones gramaticales.

Hay que decir que toda suma falsa (2 mas 3 igual a 6) es traducible a cadenas que estan bien formadas, pero que no son teoremas. No obstante la realidad y los sistemas formales son independientes entre si, a pesar de que nuestro sistema formal se fundamente en un segmento de la realidad ya que sus teoremas son isomorficos respecto a las verdades conscernientes a esa parte de la realidad. Cada una de estas esferas se sostiene por si misma, sabemos que 1 mas 1 es igual a 2, sepamos o no que -m-g– es un teorema.

Sistema determinista y sistema cuantico

Existen 2 universos: el sistema determinista (todo esta determinado y siguen unas reglas) y el sistema cuantico (analogo al primero).

Sobre un sistema formal desconocido se intentan distintas interpretaciones; si tenemos la suerte de hallar aparentemente que todo teorema es verdadero y todo no teorema es falso, esto solo se podria verificar en un numero finito de casos… lo mas probable es que la cantidad de teoremas sea infinita por lo que no sabremos que todos los teoremas que expresan verdades bajo esta interpretacion.

Numeros ideales

Pasamos ahora a hablar de los numeros ideales. No hay proceso de calculo alguno capaz de confirmar o refutar «que hay una cantidad infinita de numeros primos». (Nota personal: bucle extrano infinito?)

El teorema de euclides dice que N! + 1 solo es divisible por numeros mayores ya que si se divide por 2, 3, 4… N-1 el resto siempre sera 1. No es posible verificar de modo indirecto la veracidad de la proposicion, no obstante le damos fe, porque confiamos en el razonamiento seguido.

Si aceptamos razonar no nos quedara alternativa, pero si hemos estado de acuerdo con cada paso del Teorema de Euclides tendremos que estar de acuerdo en la conclusion de la formula, por lo que en matematicas siempre coincidiran en aceptar como verdaderas o falsas ciertas proposiciones.

El infinito

Mencionemos ahora la importancia de soslayar el infinito; para ello mediante algo finito debemos abarcar la infinitud.

Sonata para Aquiles (solo)

Descubierto el acertijo de una palabra que comienza por «la» y termina en «la», y descubierto tambien el acertijo de una palabra que contiene la cadena «vandu» en medio de una palabra. Para ambas cuestiones la palabra es «lavandula», una sola palabra cumple los dos acertijos.

En este solo, cada frase hace referencia a la anterior dando respuesta (analogamente como en matematicas donde se demuestra con pequenos saltos aunque discontinuos) a lo que se preguntaba o hablaba por la otra parte, podriamos decir que es isomorfico.

Analisis del Capitulo III: Figura y fondo.

Sistema vg

Esquema de axioma: xv-gx es un axioma, siempre que x sea una cadena de guiones.

Regla de inferencia: suponiendo que x, y y z son cadenas de guiones, suponiendo que xvygz es un teorema conocido, xvy-gzx sera un nuevo teorema.

Derivacion del teorema: – -v- – -g- – – – – –

1. – -v-g- – (axioma)
2. – -v- -g- – – – (regla de inferencia (1))
3. – -v- – -g- – – – – – (regla de inferencia (2))

Captura de compositividad

Caracterizando a los numeros compuestos definimos un nuevo conjunto de teoremas de la forma Cx.

Regla: suponiendo que x, y, y z son cadenas de guiones, si x-vy-gz es un teorema, entonces Cz tambien es un teorema.

z es un compuesto de guiones que equivale al producto de dos numeros mayores que 1, X+1 e Y+1.

Los teoremas cuentan con una forma comun porque son generados con un conjunto de reglas tipograficas, tienen los no-teoremas una forma comun por analogas razones? (Nota personal: yo creo que no, porque no pueden ser siempre isomorficos).

Figura y fondo

Figura -> espacio positivo (forma humana, letra o naturaleza muerta) + Trazada en el interior de un mero determinado -(consecuencia)->  espacio negativo.

Fondo -> espacio negativo.

Figuras (distincion canonica):

• Trazables cursivamente: aquella cuyo fondo aparece tan solo como subproducto del acto de dibujar.
• Recursivas: aquella cuyo fondo puede ser visto por derecho propio, como una figura (tanto el primero plano como el plano posterior (fondo) son trazables de forma cursiva o figura doblemente cursiva).

TNT (Teoria de los numeros tipografica)

Con la Teoria de los numeros tipografica, confiamos que nos permita caracterizar de forma analoga al conjunto de todas las proposiciones de la teoria de los numeros:

1. Como espacio novativo del conjunto de todos los teoremas TNT.
2. Como copias alteradas del conjunto de todos los teoremas TNT (producidos mediante la negacion de cada uno de los teoremas TNT).

Nota personal: figura y fondo contienen la misma informacion aunque codificada de 2 maneras complementarias? existen conjuntos recursivamente enumerables que no son recursivos y existen sistemas formales para los que no hay procedimiento tipografico de decision.

DND (Numeros demostrablemente No Dividible)

Esquema de axioma: xyDNDx, x e y son cadenas de guiones.

Regla: Si xDNDy es un teorema, xDNDxy tambien lo es.

(evitar los numeros mayores a divisores para evitar cosas como que 5 no es divisible entre 12).

Regla: Si – -DNDz es un teorema, zED- – tambien lo es.

Regla: Si zEDx es un teorema y x-DNDz es un teorema, zEDx- es un teorema.

Regla: Si z-EDz es un teorema, Pz- es un teorema.

Axioma P- – (2 es primo).

Analisis del capitulo IV: Coherencia, completitud y geometria

Significado

Si el isomorfismo es muy simple (o familiar) el significado al que nos da acceso es explicito; vemos el significado sin ver el isomorfismo. E.g. el lenguaje humano, a menudo se le da significado a las palabras mismas sin advertir del isomorfismo, que es en realidad lo que las denota de significacion. -> Falsa creencia: se cree que el ruido es un efecto colateral de toda colision de 2 objetos -> dos objetos pueden chocar sin embargo en el vacio donde no produciran sonido, existe un error al atribuir el ruido exclusivamente a la colision y en no reconocer la funcion del medio (vehiculo entre los objetos y el odio).

Nota personal: autoreferencia descubierta en la pagina 94 «me gustaria ser algo mas explicito acerca del significado explicito del relato«.

Significacion

Significacion:

• Nivel 1 -> Musica. Que es? vibraciones en el aire (primero) ? o sucesion de reacciones emocionales producidas en el cerebro (segundo) ?
• Nivel 2 -> Secuencia de vibraciones producidas en el fonografo (solo puede aparecer despues del nivel 1):
  1. 1. El isomorfismo existente entre determinada grabacion impresa en los surcos y las vibraciones del aire.
     2. El isomorfismo existente entre determinadas vibraciones del aire y vibraciones en el fonografo.
  • El significado del nivel 2 depende del encadenamiento de dos isomorfismos:

Nota personal: No se tiene en cuenta el lapso de tiempo entre la generacion de la musica (nivel 1) o primeras vibraciones mas la generacion de la segunda secuencia de vibraciones (nivel 2) y la destruccion del propio aparato que a su vez hubiera generado nuevas vibraciones en caso de no destruirse.

Incompletitud

Godel dice que ningun sistema formal por bien construido que este, puede ser perfecto. Puede ser perfecto en el sentido de reproducir toda proposicion verdadera bajo la forma de teorema.

Incompletitud: la verdad trasciende a la teoremidad en cualquier sistema formal dado que es conocido como incompletitud de tal sistema.

Sistema mg modificado

Esquema de axioma II: si x es una cadena de guiones, entonces xm-gx es un axioma. -> contendra preposiciones falsas (si tomamos las cadenas como preposiciones). E.g. – -m-g- – por ende, nuestro sistema es incoherente con respecto al mundo externo. Tambien es incongruente porque presenta dificultades internas; incoherente internamente.

-m-g- – (en el axioma anterior)

-m-g- (un axioma nuevo) -> [el hecho que los simbolos representen isomorficamente los conceptos]. Requiere interpretacion adecuada de los simbolos del sistema.

g diciendo que es «mayor o igual a» ya tenemos interpretacion significativa (la anterior seria no significativa (para el nuevo sistema, no para el sistema mg original)).

Postulados de Euclides

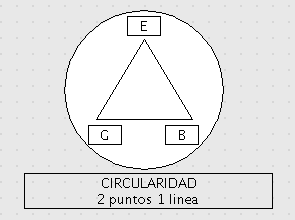
Equiv al cuarto postulado: Dada cualquier linea recta, y un punto fuera de ella, existe una y solo una linea recta que pasa a traves de este punto sin intersectar nunca con aquella linea, por mucho que se prolongue.

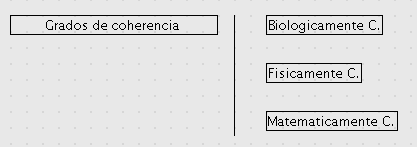
Coherencia

Mundo externo:

• Coherencia: todo teorema, al ser interpretado, deviene una proprosicion verdadera.
• Incoherencia: cuando aparece al menos 1 proposicion falsa entre los teoremas interpretados.

Mundo interno:

• Coherencia:
• Incoherencia: si 2 o mas teoremas cuyas interpretaciones son incompatibles entre si.

E.g. ajedrez: TmZ ZmE EmT } coherencia interna aunque no sea verdadera (coherencia externa) sino compatibles entre si los teoremas (coherencia interna).

E.g. invento: TmZ ZmE EmT } No tiene coherencia interna.

Sistemas formales dentro de sistemas formales

Aritmetica de peano -(completitud)-> Teoria de los numeros absoluta.

Completitud

Coherencia: cuando los teoremas, al ser interpretados resultan verdaderos (en algun mundo imaginable).

Completitud: cuando todas las proposiciones que son verdaderas (en algun mundo imaginable) pueden ser expresadas como cadenas bien formadas del sistema son teoremas.

Pag. 114 repasar definiciones asi como el concepto de demostrable.

Pequeno laberinto armonico

En este capitulo se explica el concepto de pila. Pero quiza, lo que sea mas interesante no solo es cuando explica el concepto de sacar o meter y entrar asi en nuevas dimensiones, sino la comunicacion entre distintos cuadros una vez se entra. Tambien se puede ver el concepto de «scope» una vez se entra o se sale de una, se pierde visibilidad de otras dimensiones.

Por otra parte el concepto de pila es de uso cuotidiano y aunque lo apliquemos dia tras dia no nos damos cuenta debido a la trivialidad del proceso cuando se efectua de manera habitual todos los dias, solo lo percibimos y podemos cercionarnos de el cuando se emplean en distintos topicos en cada capa, pero como en el dialogo de Aquiles y La Tortuga, donde ellos mismos son los protagonistas de un Mundo paralelo, ya sea en un cuadro, dentro de un libro, o dentro de la imaginacion de la imaginacion de los personajes, es realmente complejo saber en que Mundo se encuentra uno y es realmente dificil distinguir en que dimension se encuentra uno.

En todos estos dialogos, podemos tambien ver la recursividad aplicada en nuestro Mundo (o las ideas dentro de ideas (que pueden a su vez estar dentro de otras ideas)) y es asi senores, como se emplea el uso del parentesis para describirse y autoreferenciarse asi misma, una idea.

Notese que los conceptos de Mundo, dimension, capas y ambito (o scope) no son apropiadamente usados en mis anotaciones y tan solo sirve como una referencia inexacta pero que ayuda a comprender sin entrar en muchos detalles la idea que se intenta expresar.

<en desarrollo>